Separating Reality from Hype - Quantum Computing Explained
Quantum computers are hyped to the moon and back. To date, there hasn’t been a useful quantum computer built despite all the talk and billions in investment. Today, we want to cut through the overhype regarding quantum computers and explain the realities of the quantum computing industry. This report will discuss the uses of quantum computing, what it takes to build a useful quantum computer, and why that is still very far away.
We will also discuss the qubit counting nonsense and why the marketing heads jockeying for the highest qubit quantum computer are making fools of themselves. Furthermore, we will discuss the impacts of quantum computers on the classical computing industry, which are already being felt across the industry, primarily regarding new encryption schemes.
Special thanks to the SPIE Lithography and Patterning and the SPIE Optics and Photonics, which helped us research this topic and provided many images. Special thanks to the Domain of Science for providing excellent in-depth research.
Quantum Computing Basics – Entanglement, Superposition, Interference
In order to understand why quantum computers could be faster than classical computers, it's essential to understand the difference between bits and qubits.
In classical computing, a bit is the basic unit of information. It can represent either a 0 or a 1.
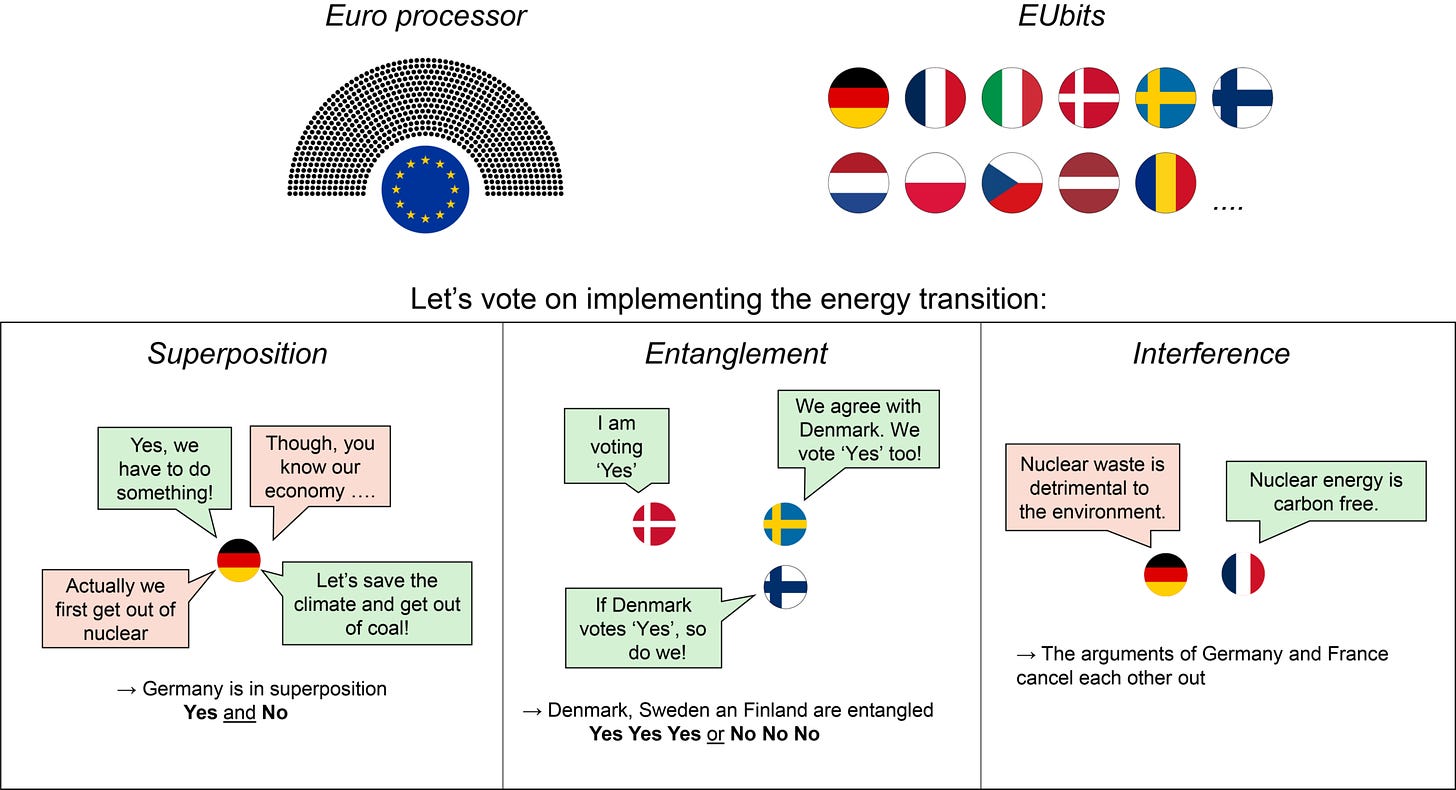
In contrast, a qubit is the basic unit of information in quantum computing. A qubit is not limited to representing just a 0 or a 1. Instead, it can represent a combination of both 0 and 1 at the same time. This is called superposition. This means that a qubit can be in a range of probabilities for 0 and 1 at the same time. However, when the qubit is measured, it will only output either a 0 or a 1 based on those probabilities.
So, while a classical computer can only be in one of two states at a time, a quantum computer can be in a superposition of many states at the same time. This is what gives quantum computers their advantage: they can explore many different possibilities simultaneously, rather than having to try them one by one like a classical computer.
Now, let's consider how the number of states that a classical computer can be in affects its performance. In a classical computer, the number of states grows by a power of 2 for each bit added. For example, if you have one bit, you can represent two states (0 or 1). If you have two bits, you can represent one of four states (00, 01, 10, or 11). If you have three bits, you can represent one of eight states (000, 001, 010, 011, 100, 101, 110, or 111), and so on.
In contrast, the number of states a quantum computer can be in grows exponentially with the number of qubits. For example, if you have two qubits, you also have four states (00, 01, 10, or 11), just like a classical computer with two bits, but the quantum computer can represent all 4 of them at once due to the bits being entangled. If you have three qubits, you can represent eight states (000, 001, 010, 011, 100, 101, 110, or 111) plus all the superpositions of those states. This means that the number of states a quantum computer can represent grows exponentially faster than a classical computer can represent.
This is why quantum computers are so powerful; they can explore a vast number of states simultaneously, allowing them to solve specific problems much faster than classical computers. Classical computers can be in any number of states, but it is always only one at a time.
Now enjoy this awesome image from Valentin John, which explains superposition and entanglement with a highly topical/political joke scenario of the EU.
The last important central concept to understand is interference. Each qubit is actually a representation of a quantum wave function. A quantum wave function is a mathematical description of everything in quantum mechanics. It describes the probability of finding a particle in a particular location or having a particular energy or spin.
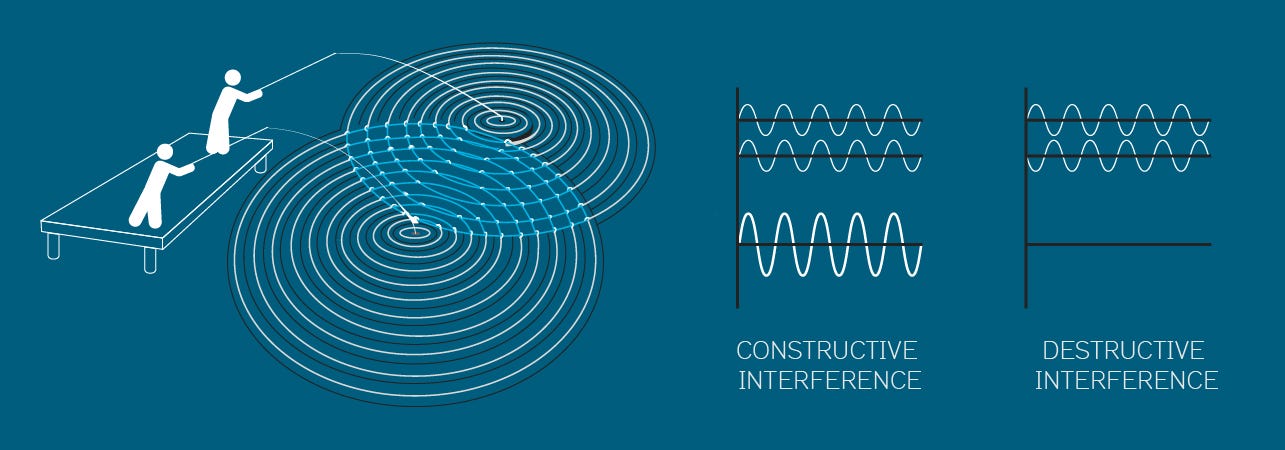
When the qubits are entangled, their wave functions are added together into an overall wave function describing the quantum computer’s state. This adding together of wave functions is called interference.
Like with waves in water, when we add quantum waves together, they can constructively interfere and add together to make a bigger wave (amplify), or destructively interfere and cancel each other out (suppress). In a quantum computer, the overall wave function sets the different probabilities of the different states. By changing the states of different qubits, we can change the probabilities that different states will come out when we measure the quantum computer.
Theoretically, by carefully manipulating the states of different qubits, quantum computers can use interference to change the probability distribution and solve problems much faster than classical computers.
This is why interference is so important in quantum computing: it allows us to use the superposition of many states to increase the probability of the correct answer and decrease the probability of the incorrect answers, so that when we measure the quantum computer and collapse all the various states and have only 1 state outputted, the correct answer is more likely to be the one that we get from the computer.
Quantum Algorithms and Uses
A quantum algorithm is a specific method for using a quantum computer to solve a problem. Quantum algorithms are designed to take advantage of the unique properties of quantum computers, such as superposition and entanglement, to solve problems faster than classical algorithms. While there are many different quantum algorithms, we want to focus on a few key ones.
The most famous is Shor’s algorithm, which is a quantum algorithm that can factorize large numbers much faster than any classical algorithm. Factoring a number means finding the prime numbers that, when multiplied together, give you the original number. For example, the prime factorization of the number 15 is 3 and 5, because 3 x 5 = 15.
Multiplying numbers is very easy and cheap in hardware with classical computers on modern semiconductors, even as the size of numbers grows. In contrast, factoring becomes exponentially more difficult for classical computers with each additional digit in the number being factored. In comparison, Shor’s algorithm scales polynomially rather than exponentially with increasing complexity in the factorization problem.
Shor’s algorithm works by using quantum superposition and quantum entanglement to simultaneously explore many different possible factorizations of the number. Interference is then used to amplify the probabilities of the correct factorizations and suppress the probabilities of the incorrect ones. When the quantum system is measured, the correct factorization is much more likely to be the outcome.
This is important because the RSA encryption algorithm relies on the fact that it is currently very hard for computers to factorize large numbers. Many other encryption and hashing algorithms suffer the same fate as RSA. Cryptography is what enables security in our lives, whether it’s secures websites, emails, or bank accounts.
While modern encryption means it’s basically impossible to crack bank accounts, top military secrets, or your secure connection to www.SemiAnalysis.com with classical computers. Theoretically, a quantum computer with ~1,000,000 qubits could break encryption algorithms such as AES 256 in a few months. As such, 4 quantum-resistant standards are being proposed and ratified by the National Institute of Standards and Technology for classical computers.
Some could be needed sooner than others, but the important thing is that most processors being sold will contain acceleration blocks for these new standards. Classical computers can still use the new encryption standards, but if quantum computers work at any time in the next decade or two, they won’t be able to crack them. These new encryption standards are incredibly important as insurance, government, banking, and health-related information is often stored for extremely long periods of time, which means if it is encrypted today, it could be cracked 20 years from now and still be useful data.
There are quantum algorithms that are suited to many other problems in physics, chemistry, simulation, and data search/sort. There are also many uses within the field of AI. At the bleeding edge of semiconductor device fabrication and patterning, the role of quantum computing could take on several incarnations, from looking at the electron dynamics to EUV photoresist secondary electrons effects during exposure to interface simulation and engineering for emerging memories or advanced CMOS, to process analytics for the entire fab.
It is noteworthy that not all problems are better on quantum computers as they run different algorithms than classical computers. It is also noteworthy that no useful quantum computers exist yet despite marketing claims.
Building A Useful Supercomputer
There are many ways companies and startups are attempting to build a quantum computer, but regardless, they grapple with the same issues. The primary one is that the qubits need to be entangled with each other and nothing else outside the system. When the system is observed, it loses its quantum state and collapses to the final answer kind of like Schrodinger’s Cat. If the qubit has interactions with the outside world, the model will be affected, and decoherence creeps in.
Qubits can be affected by minor levels of electromagnetic radiation, including cosmic rays, temperature, or mechanical vibrations. These interactions cause the qubits to lose their quantum properties, which can result in errors in the computation. The biggest challenge is how do you physically make a device that is completely shielded from the rest of an environment while it is running, but also physically controllable and measurable. Furthermore, this noise becomes more and more difficult to block as you add more Qubits to a system. The reality we have to accept is that there will be noise.
Furthermore, there are many complexities with manufacturing qubits as well. The above image is an analogy the CEO of PsiQuantum likes to make. A qubit is a lot like the idea of a burger in commercials. In reality, you will not receive anything close to what is advertised when you go out and buy a burger from a chain that was advertising it on TV.
There is no single process in the world with atomic precision 100% of the time for a complex device. The only industry in the world that gets even close is the semiconductor industry, but there are significant difficulties and challenges regardless. The semiconductor industry has a huge degree of yield harvesting and binning to compensate for imperfections in manufacturing. Qubits are even more sensitive to any variation in the manufacturing process, given that they rely on quantum phenomena.
The reality is that it is hard to entangle these qubits, and they will lose their coherence quickly due to interference. The classical computing industry uses many redundant structures such as cores, interconnects, SRAM, and ALUs. The quantum industry needs an even larger degree of redundancy due to their sensitivity.
Marketing will constantly claim “quantum supremacy” with a qubit number that would theoretically surpass classical computers at many operations, but these cannot be entangled for any reasonable duration. Once interference sets in and coherence is lost, the data is worthless, and the algorithm achieved no useful work. Error rates are very high when each physical qubit represents a logical qubit in your quantum computer.
Instead, quantum computers need between 1,000 to 100,000 physical qubits entangled together to represent 1 noise-free qubit. This noise-free qubit has a significantly lower error rate and, therefore, can operate for many more clock cycles. Real computing could potentially be done. Even at the low end of estimates, the reality is it will take over a million qubits in a quantum computer to complete any useful work.
Regardless of the approach, noise from the outside world must be minimized; hence nearly every quantum computing approach attempts to operate at as close to 0 kelvin as possible. The problem with these cryogenic-cooled approaches is that when the computer is scaled to over a million qubits, what does that system look like.
The key takeaway is that the number of qubits is not relevant to watch, but rather the error rates.



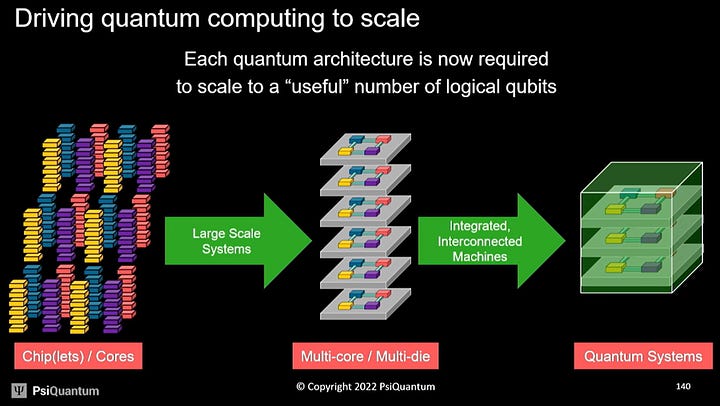
Dozens of companies believe their approach to a quantum computer is scalable. Each has a different quantum computing model and/or material choices. We aren’t experts on the various types and methods, so we will cover PsiQuantum’s approach as it helps frame major ideas when thinking about other firms’ approaches. There are going to be pros and cons with each approach.
PsiQuantum’s argument is that most quantum approaches rely on the electrical domain, which may work better on a small scale, but cannot scale to millions of qubits. Millions of qubits means a system with many chips and networking in between. The networking would also need to be cryogenically cooled and shielded to protect from outside interference.
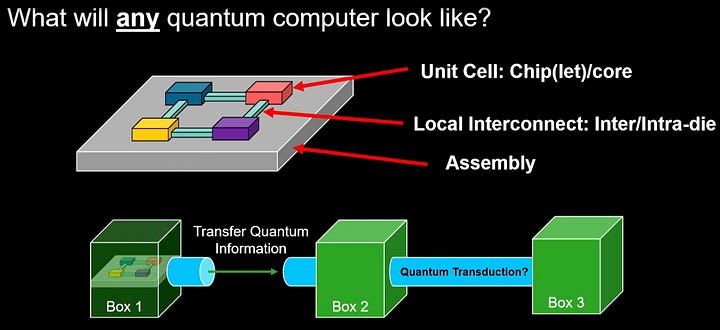
Photons are theoretically much easier to protect from interference when networking to other chips and systems. If computing is done in the electrical domain and networking in the optical domain, then that necessitates electro-optical devices to translate. These electro-optical devices would introduce another avenue of interference, so the computing and data movement must all be done in the optical domain.
Because computing and networking is done in the optical domain, PsiQuanutm argues that their systems can operate at more normal temperatures than quantum computers operating in the electrical domain. Their systems are still currently in the single-digit kelvin range but compared to other quantum computers, which are pushing into the milli-kelvin range, that is much easier to achieve.
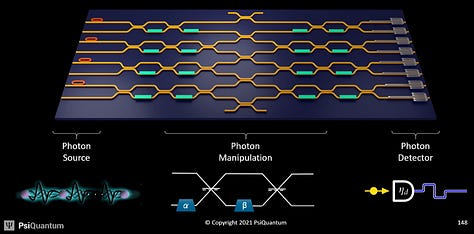
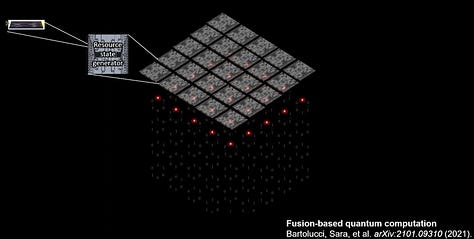
Getting photons to interact with each other or entangle is very difficult, and that is one of the primary challenges PsiQuantum faces. PsiQuantum controls their qubits with micro-ring resonators. There are many challenges in manufacturing micro-ring resonators given even a nanometer of variation in the structure will change the way it operates. That discussion will be included in the supplementary section.
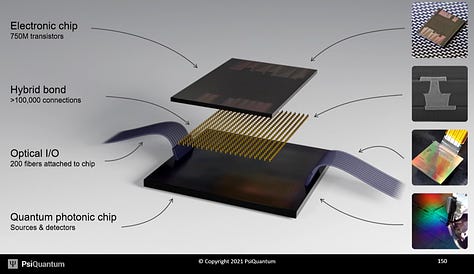
PsiQuantum also argues they don’t need as low-temperature of a system either. PsiQuantum’s approach also utilizes interesting technologies, such as hybrid bonding and co-packaged optics, through their partner, GlobalFoundries. This partnership is very interesting in the foundry space because PsiQuantum bought tools and installed at GlobalFoundries manufacturing facilities. This is very unique for a normal foundry relationship at GlobalFoundries, TSMC, etc.
The supplementary section of this report shares slides and transcripts regarding PsiQuantum specifically. The topics covered in those slides and transcripts will include lithography, etch control, patterning challenges, edge placement error, cryogenic operations, superconductivity, scalability, interconnects, automated test equipment, layout, optical proximity correction, SiN material control, and the 200mm to 300mm transition for building quantum computers.